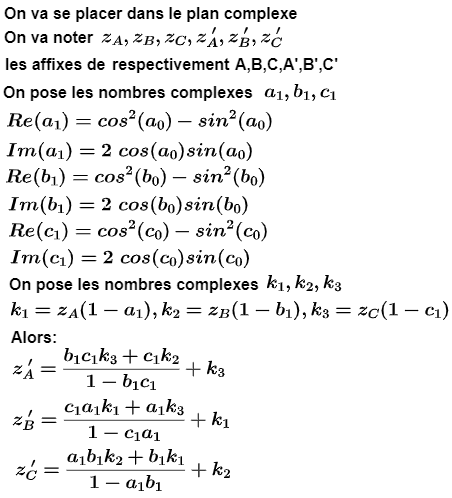Résultat du test :

Auteur : aerobase
Date : 20 oct.23, 04:25
Message :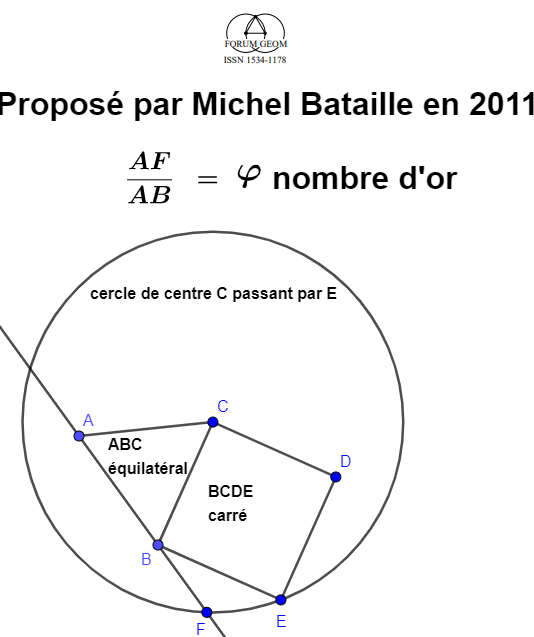

Auteur : J'm'interroge
Date : 20 oct.23, 04:28
Message :

aerobase a écrit : 20 oct.23, 04:25

Pas mal !

Je ne connaissais pas cette construction.
.

Auteur : aerobase
Date : 20 oct.23, 04:43
Message :

J'm'interroge a écrit : 20 oct.23, 04:28 Pas mal !
Je ne connaissais pas cette construction.
.

Moi non plus
C'est de quelqu'un qui vivait à Rouen en 2011
ça date de 2011 sur un site de l'université Florida Atlantic University
https://www.fau.edu/

Auteur : indian
Date : 20 oct.23, 04:56
Message : peut on y ajouter un pentagone?

Auteur : aerobase
Date : 20 oct.23, 05:03
Message : Pourquoi pas Indian (il est chez lui)

Auteur : J'm'interroge
Date : 20 oct.23, 23:17
Message : .




https://forumgeom.fau.edu/FG2011volume11/FG201106.pdf




.

Auteur : prisca
Date : 21 oct.23, 02:56
Message :

aerobase a écrit : 20 oct.23, 04:25

Auteur : aerobase
Date : 21 oct.23, 07:11
Message : Ah faut croire Prisca

Auteur : J'm'interroge
Date : 21 oct.23, 13:12
Message : Ça n'a rien à voir mais je trouve que le 5ième terme de la fraction continue de Pi est étonnamment grand :

Pi = [3,7,15,1,292,1,1,1,2,1,3,1,…]

Auteur : aerobase
Date : 24 oct.23, 03:15
Message : sinon à part ça

Auteur : J'm'interroge
Date : 24 oct.23, 03:21
Message : .

Merci,

Je ne connaissais pas les cercles d'Apollonius ni les divisions harmoniques de segments.

Propriété intéressante de ce cercle.

.

Auteur : aerobase
Date : 24 oct.23, 03:31
Message : on prend un segment [AB] et on se donne un scalaire "s" ici dans cet exemple on a pris s le nombre d'or
Alors il existe un cercle appelé cercle d'Apollonius du triplet (A,B,s) tel que pour tout point M de ce cercle alors
MA/MB=s

Le calcul (géométrie analytique) de ce cercle se simplifie quand le scalaire "s" est le nombre d'or

Auteur : aerobase
Date : 25 oct.23, 11:40
Message : Dans ce sujet, Michel Bataille nous propose de construire le nombre d'or
à partir d'un triangle équilatéral
Par Frank Morley https://fr.wikipedia.org/wiki/Frank_Morley
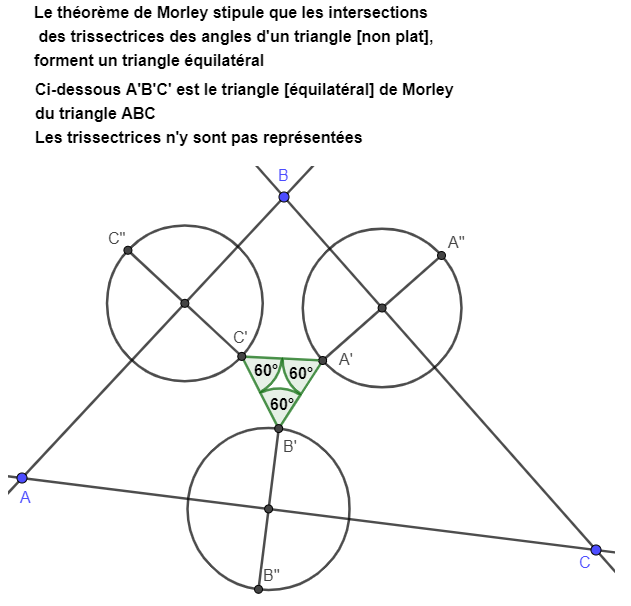
On se propose de faire correspondre un triangle équilatéral
à un triangle non plat quelconque en utilisant le théorème de Morley
On va utiliser la démonstration du théorème de Morley
donnée dans ce lien http://www.numdam.org/item/PMIHES_1998__S88__43_0.pdf
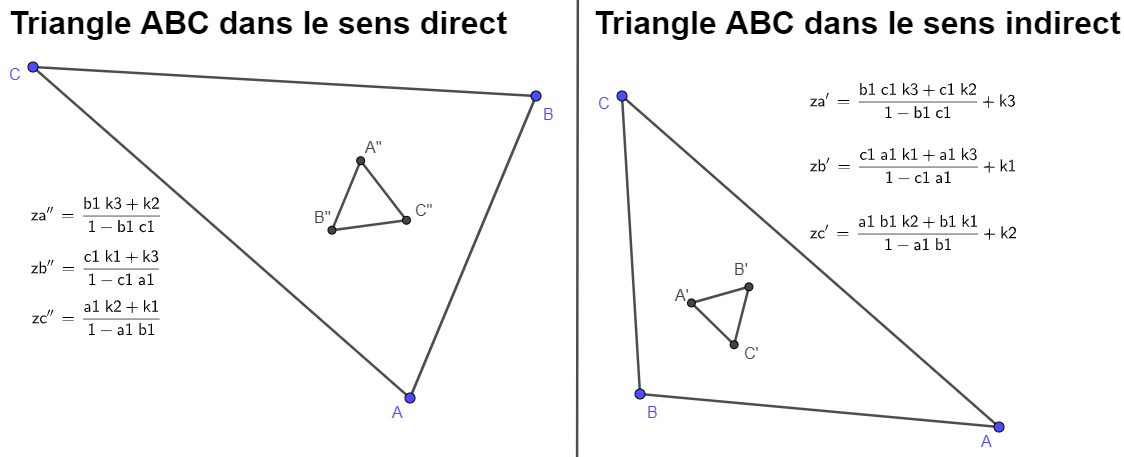
par Alain Connes en 1998 pour déterminer les affixes respectivement za',zb',zc'
des sommets respectivement A',B',C' du triangle de Morley A'B'C' du triangle ABC

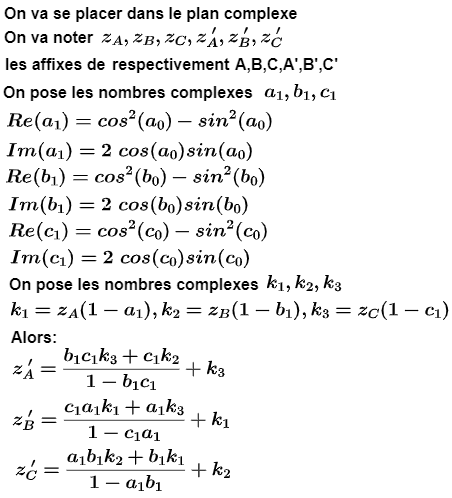
Auteur : J'm'interroge
Date : 26 oct.23, 09:53
Message : Up !

Auteur : aerobase
Date : 26 oct.23, 09:57
Message : Merci JMI
Les formules des affixes des sommets du triangle de Morley
dépendent du sens (direct ou indirect) du triangle ABC

Auteur : lafrisée
Date : 30 nov.23, 21:16
Message : https://www.lafleurcurieuse.fr/culture/ ... ombre-dor/

"Dans de très nombreuses cultures et religions existent en réalité des représentations de la pomme de pin. D’abord dans des sculptures assyriennes de 713 avant Jésus-Christ. Au Mexique, une statue du dieu mexicain Chicomecoatl offrant des pommes de pin dans une main.
Dans la mythologie grecque, puis romaine, le thyrse est un grand bâton évoquant un sceptre surmonté d’une pomme de pin.
A cela s’ajoute l’enfant de la Vierge noire de Montserrat qui détient dans l’une de ses mains … une pomme de pin. Tout comme Shiva, le dieu Hindoue et sa chevelure enroulée telle une spirale ou même encore l’éclairé Bouddha dont le crâne évoque… une pomme de pin…

https://echo-bat.fr/2018/08/06/acoustiq ... ombre-dor/

"Ce bref parcours est la première ébauche d’une étude plus fouillée. Mais ces quelques lignes vous permettront déjà de percevoir quelques enjeux qui transparaissent… Nous appliquons cette étude dès lors que nous intervenons pour le réglage acoustique des édifices religieux (églises ou abbayes)."

Auteur : J'm'interroge
Date : 03 déc.23, 10:36
Message : La pomme de pin est un symbole de la glande pinéale, laquelle est parfois considérée comme le "troisième oeil". D'ailleurs c'est bien structurellement un oeil et c'est un oeil vestigial. À savoir que Nos lointains ancêtres batraciens avaient trois yeux, et aujourd'hui encore certaines espèces de reptiles comme le basilique et certains iguanes possèdent encore cet organe à la surface de leur crane, organe sensible à la lumière. Chez nous humains, selon certains, Descartes lui-même a d'ailleurs fait des recherches à ce sujet, elle serait le point de contact entre le corps et l'esprit.